117.	Kakve su to prisilne vibracije s prigušenjem?

 

    U realnim se sustavima susreću vrlo često prisilne vibracije s prigušenjem. Čestica je vezana oprugom karakteristike  za nepomični oslonac te prigušnim elementom s konstantom viskoznog prigušenja k.

    Na česticu djeluje vremenski promjenjiva sila:  gdje je F_o amplituda poremećajne sile, a s poremećajna kružna frekvencija.

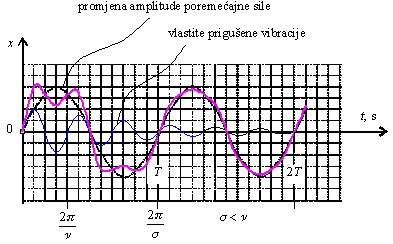
    Čestica će se gibati harmonijski kako je već opisano u prethodnom poglavlju, ali u ovom primjeru uz djelovanje prigušnog člana.

    Ako se u nekom trenutku slika b), čestica oslobodi veza, a veze zamijene silama, tada se mogu postaviti jednadžbe kinetičke ravnoteže (D'Alembertov princip) prema slici c):

 

    , slijedi  te nakon uvrštenja slijedi:

    .

    Opće je rješenje ove diferencijalne jednadžbe:

    .

    Ovdje je n vlastita kružna frekvencija prigušenih vibracija, a  amplituda prisilnih vibracija.

    Može se uvesti oznaka  koja se naziva bezdimenzijski omjer prigušenja, gdje je
     kritično prigušenje te je tada
    bezdimenzijski omjer prigušenja .

    Kritična će frekvencija biti  uz kritičnu amplitudu .

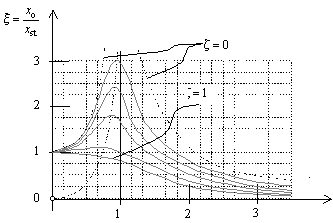
    Faktor povećanja amplituda (magnifikacija amplituda) važna je značajka koji prikazuje slika čiji je analitički izraz: .

 

 

     Prisilne torzione vibracije s prigušenjem

 

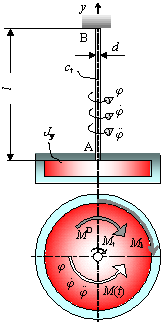
    U svrhu analize torzionih vibracija s prigušenjem može se postaviti sustav kao na slici.

    Utjecaj se prigušenja može predstaviti kao uljna kupka oko diska koji vibrira. Otpor se gibanju diska može pretpostaviti moment , N×m, proporcionalan kutnoj brzini.

    Na disk djeluje vremenski promjenjivi zakretni moment:

     gdje je M_o, N×m, amplituda poremećajnog momenta, a s, rad/s, poremećajna kružna frekvencija.

 

    Jednadžba će kinetičke ravnoteže oko osi y ovdje glasiti:

 

    ,    .

    Analiza pokazana pod d) ovdje je posve analogna.