139.	Kako se određuje ubrzanje točke tijela pomoću metode plana ubrzanja?

 

Ovo je grafičko-analitička metoda. Moguća su dva slučaja rješavanja:

 

a)	POZNATO:
	-	geometrija tijela (položaj točaka i drugo) i brzine točaka tijela,
	-	ubrzanje jedne točke (npr. A) i pravac ubrzanja za točku (npr. B) za koju treba odrediti ubrzanje.
	TRAŽI SE:
	ubrzanje točke B, kutno ubrzanje tijela.

 

b)	POZNATO:
	-	geometrija tijela (položaj točaka i drugo) i brzine točaka tijela,
	-	kutno ubrzanje tijela i pravci ubrzanja za točke (npr. A i B) za koje treba odrediti ubrzanja.
	TRAŽI SE:
	ubrzanja točaka A i B.

 

Pristup rješavanju je takav, da se prvo u mjerilu nacrta crtež koji se zove Plan položaja.

 

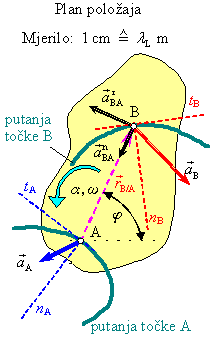
Kako su u predloženom primjeru putanje točaka A i B krivulje, to će ubrzanja obiju točaka imati i normalnu i tangencijalnu komponentu.

 

Vrijedi relacija:

.

gdje su u donjem retku istaknuti smjerovi pojedinih komponenti.

 

    Primjer rješenja slučaja a):

 

U ovom je slučaju poznat vektor ubrzanja , ali su isto tako poznati iznosi i smjerovi normalnih komponenti ubrzanja jer su poznate brzine i geometrija gibanja tijela, a to znači i polumjeri zakrivljenosti r_A i r_B putanja točaka A i B.

Dakle, može se izračunati:

 te slično tomu .

Smjer je normalne komponente ubrzanja  UVIJEK od točke B k središtu zakrivljenosti putanje točke B.

Smjer je normalne komponente ubrzanja  UVIJEK od točke B k točki A.

 

Nepoznati su iznosi komponenti ubrzanja  i .

Pravci ovih tangencijalnih komponenti ubrzanja su UVIJEK okomiti na istoimene normalne komponente.

 

Potrebno je sada crtati drugi crtež u mjerilu koje se zove Plan ubrzanja.

 

Zapravo, pri ovom se crtanju gotovo uvijek radi o KONSTRUIRANJU poligona s n stranica koje mu su poznate duljine dužina  stranica, kao i svi pravci komponenti ubrzanja.

 

Redoslijed crtanja (slika):

-         u planu se ubrzanja odabere pol plana ubrzanja ,

-         paralelno se iz plana položaja ucrta ubrzanje ,

-         u ovom vektorskom zbroju  s desne je strane poznata komponenta  te se kroz njen vrh povuče smjer  tangencijalne komponente,

-         s lijeve je strane ovog vektorskog zbroja poznata komponenta  te se kroz njen vrh povuče smjer  tangencijalne komponente,

-         Ubrzanja svih točaka tijela imaju polaznu točku u polu plana ubrzanja .

 

Kako je po definiciji  to se može odrediti kutno ubrzanje tijela: .

    Primjer rješenja slučaja b):

 

U ovom je slučaju poznato kutno ubrzanje tijela a, ali su isto tako poznati iznosi normalnih komponenti ubrzanja jer su poznate brzine i geometrija gibanja tijela, a to znači i polumjeri zakrivljenosti r_A i r_B putanja točaka A i B.

Dakle, može se izračunati:

 i  te slično tomu  kao i .

Nepoznati su iznosi (ali poznatih smjerova) komponente ubrzanja  i .

 

Potrebno je sada crtati drugi crtež u mjerilu koje se zove Plan ubrzanja.

 

Zapravo, pri ovom se crtanju gotovo uvijek radi o KONSTRUIRANJU poligona koje mu su poznate duljine dužina  stranica, ali i svi pravci komponenti ubrzanja.

 

 

Redoslijed crtanja (slika):

-         u planu se ubrzanja odabere pol plana ubrzanja ,

-         paralelno se iz plana položaja s početkom u polu  ucrta jedino poznata komponenta ubrzanja  i u njenom vršku pravac  tangencijalne komponente ubrzanja ,

-         u ovom vektorskom zbroju  s lijeve je strane zbroja poznata jedino komponenta  s početkom u polu  te se kroz njen vrh povuče smjer paralela s  tangencijalne komponente ,

-         u tom vektorskom zbroju  s desne strane, poznate su i obje komponente  i . Može se zaključiti iz ove vektorske jednadžbe da komponenta  treba polaziti iz vrška  te da komponenta  treba završiti u vršku .
Dakle, potrebno je konstruirati zbroj  tako da vršak tangencijalne komponente  završava ne pravcu  kojim će biti na koncu povučena komponenta . S druge pak strane, početak komponente  je u vršku . Sada je potrebno sukladnim pomicanjem pomaći zbroj  tako da vršak  "putuje" po pravcu  a početak komponente  "putuje" po  do točke gdje se pravac  presijeca s pravcem .

-         Ubrzanja svih točaka tijela (ovdje A i B:  i  ) imaju UVIJEK polaznu točku u polu plana ubrzanja .