Za sve vrste materijala u dijagramima rastezanja (odnosno sabijanja ili smicanja) postoji područje proporcionalnosti naprezanja i deformacija, na slici označeno plavom bojom. Npr. kod rastezanja epruvete postoji mjerni dio koji je jednoliko opterećen na rastezanje, slika. Početna duljina mjernog dijela epruvete povećala se za , a promjer smanjio se za . Kod rastezanja je i , dok je kod sabijanja suprotno, tj. i .
Prosječne deformacije su jednake pravima, te se sa označuje uzdužna duljinska deformacija, a sa poprečna duljinska deformacija mjernog dijela epruvete .
Pokusi na mjernim epruvetama pokazuju da pri malim deformacijama postoji proporcionalnost između opterećenja i produljenja , odnosno između naprezanja i uzdužne duljinske deformacije , te također između uzdužne i poprečne duljinske deformacije.
Matematički se ovisnost između naprezanja i uzdužne duljinske deformacije , može izraziti pomoću Hookeovog zakona za jednoosno stanje naprezanja (1687.):
,
gdje je faktor proporcionalnosti - (Youngov) modul elastičnosti materijala,
a uzdužna duljinska deformacija jest: ,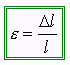
gdje je početna duljina, a je produljenje mjernog dijela epruvete.
Pokusi sabijanja daju slične dijagrame kao kod pokusa rastezanja, pa Hookeov zakon vrijedi i za tlačna naprezanja.